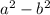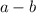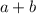Answer:
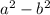
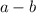
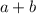
Explanation:
The given expression that represents the volume of the rectangular prism is:

We can rewrite this to reveal a perfect square pattern.
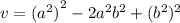
We factor using perfect squares to obtain:
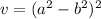
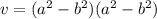
Volume is three dimensional so we need a third factor different from 1.
We further factor one of the difference of two squares to get:
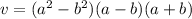
So pick the following unique dimensions from the possible answers: