Question

What is the total concentration of an acetic acid solution (ch3cooh) with a ph of 3.5? acetic acid ka = 1.76 x 10-5 m?

Answer 1

The dissociation reaction of acetic acid is as follows:

`CH_(3)COOH\leftrightharpoons CH_(3)COO^(-)+H^(+)`

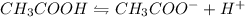
The acid dissociation constant K_{a} is
`1.76* 10^(-5)`.

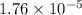Let the initial concentration of acid be A, and concentration of
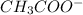`CH_(3)COO^(-)` and
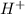`H^(+)` be zero.

After dissociation, concentration of acid becomes A-x and that of both
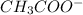`CH_(3)COO^(-)` and
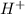`H^(+)` becomes x.

Expression for acid dissociation constant will be:

`K_(a)=([CH_(3)COO^(-)][H^(+)])/([CH_(3)COOH])`

pH of solution is 3.5, thus, concentration of hydrogen ion can be calculated as follows:

`pH=-log[H^(+)]`

On rearranging,

`[H^(+)]=10^(-pH)=10^(-3.5)=0.0003162`

Since,
`[CH_(3)COO^(-)]=[H^(+)]=x`

Thus,

`[CH_(3)COO^(-)]=0.0003162`

and,
`x=0.0003162`

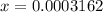
Putting the values, in expression for acid dissociation constant,

`1.76* 10^(-5)=((0.0003162)(0.0003162))/([CH_(3)COOH]_(initial)-0.0003162)`

On rearranging,

`[CH_(3)COOH]_(initial)=((0.0003162)* (0.0003162))/(1.76* 10^(-5))+0.0003162=0.006`