we are given
position function as
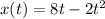
we know that acceleration is second derivative of position
so, firstly, we will find first derivative
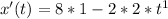
now, we can simplify it
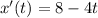
now, we can find derivative again
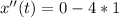
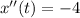
now, we can plug t=2
and we get
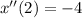
so,
the value of the person’s acceleration a at t=2s is -4..........Answer