Question

How to know when there is a vertical dilation or a horizontal dilation?

Answer 1

Given a function
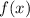`f(x)` and a number
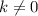`k\\eq 0`, if you multiply the whole function by
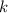`k`, you have a vertical dilation:

`f(x) \to kf(x) = \begin{cases} \text{vertical dilation} & \text{ if }k>1\\\text{vertical compression} & \text{ if }0<k<1 \end{cases}`

If
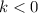`k<0`, you follow the same steps as before, but you also reflect the function around the x-axis.

If, instead, you multiply only the argument by
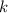`k`, you have a horizontal dilation:

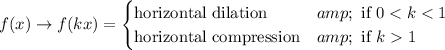
`f(x) \to f(kx) = \begin{cases} \text{horizontal dilation} & \text{ if }0<k<1\\\text{horizontal compression} & \text{ if }k>1 \end{cases}`

If
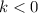`k<0`, you follow the same steps as before, but you also reflect the function around the y-axis.