Question

Point a pq and r are collinear on pr and pq: pr =2/3. P is located on the origin q is located at (x,y) and r is located at (-12,0) . What are the values of x and y

Answer 1

The values of x and y are 8 and 0 respectively.

Step-by-step explanation

As 'p' is located at (0,0) and 'r' is located at (-12,0) , that means both 'p' and 'r' are on the x-axis. So point 'q' will be also on the x-axis , and 'q' is located at (x,y)

So, the value of y will be 0. That means the co ordinate of point 'q' is (x, 0)

Now, using the Distance formula, length of 'pq'
`= √((x-0)^2 +(0-0)^2)= √(x^2)= x`

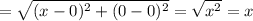
and length of 'pr'
`= √((-12-0)^2+(0-0)^2)= √(144)=12`

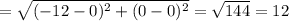
Given that, pq : pr =2/3

So....

`(x)/(12) =(2)/(3)\\ \\ 3x=24\\ \\ x= (24)/(3)=8`

Thus, the values of x and y are 8 and 0 respectively.