The given expression is

And in the second factor, x is common. So on taking x out, we will get
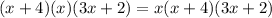
We can expand it by distributing , that is
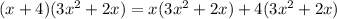
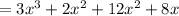
Combining like terms,
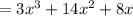
And that's the expanded form ., and the given expression can also be written in that way .