Since both machines maintain their rate, the number of copies made and the elapsed time are proportional. This means that we can write a proportion like
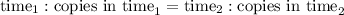
We know the performance of machine a for 12 minutes, and we want those for 30 minutes: the proportion becomes
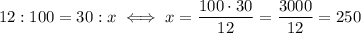
Similarly, we have for machine b
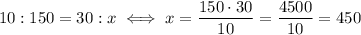
So, together, the two machines make
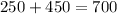
copies.