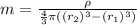Question

What mass of a material with density ρ is required to make a hollow spherical shell having inner radius r1 and outer radius r2? (use any variable or symbol stated above as necessary.)?

Answer 1

Answer:
`m=\frac {\rho}{(4)/(3) \pi( (r_2)^(3) - (r_1)^(3)) }`

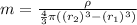
It is given that:

Density of material =ρ

radius of inner spherical shell =
`r_1`

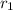
radius of outer spherical shell=
`r_2`

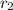
we know that the volume of sphere is
`(4)/(3)\pi r^(3)`

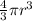
Volume of the given spherical shell =
`(4)/(3)\pi( (r_2)^(3)-(r_1)^(3))`

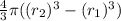
Then mass of the spherical shell can be calculate as:

Mass, m=density/ volume

`m=\frac {\rho}{(4)/(3) \pi ((r_2)^(3) - (r_1)^(3)) }`