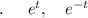Question

The solutions to the linear differential equation d2u/dt2 = u form a vector space (since combinations of solutions are still solutions). find two independent solutions, to give a basis for that solution space.

Answer 1

Serious high school. This is one of the few differential equations I can solve.

The usual particular solution is
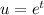`u=e^t` because
`e^t` is its own derivative.

An independent solution is
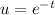`u=e^(-t)` which has a negative sign in the first derivative which turns back to positive in the second.

The arbitrary linear combination spans the solution space:

`u= c_1 e^t + c_2 e^(-t)`

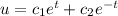
But we only are asked for the basis.

Answer:
`\textrm{. } \quad e^t, \quad e^(-t)`