Question

Exactly 0.1 of the radioactive nuclei in a sample decay each hour. thus, after n hours, the fraction of nuclei remaining is (0.900)n. find the value of n equal to one half-life.

Answer 1

It has been given that exactly 0.1 of the radioactive nuclei in a sample decay each hour. Thus, after n hours, the fraction of nuclei is given by the model expression:
`(0.900)^n`.

Now, to find the value of n equal to one half-life, all that we need to do is to equate the above expression to half or 0.500 (to the indicated places of decimal) and solve for n.

Thus, we will get:

`(0.900)^n=0.500`

Taking the log to the base 10 on both sides, we get: (Please note that we can take the log to any base)

`n* log(0.900)=log(0.500)`

Dividing both sides by log(0.900), we get:

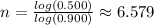`n=(log(0.500))/(log(0.900))\approx6.579`hours

Therefore the value of n equal to one half-life is 6.579 hours.