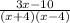So firstly, we will be using the difference of squares with the second fraction's denominator. The difference of squares is
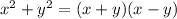 . Apply this rule to this expression:
. Apply this rule to this expression:

Next, we have to find the LCM, or least common multiple, of both denominators. In this case, the LCM is (x + 4)(x - 4). Multiply the denominators with the quantity that gets the LCM as the denominator, and then multiply by that same amount on their numerators:
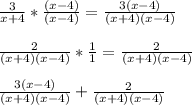
Now foil 3(x - 4):
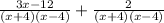
And lastly, add the numerators up and your final answer will be