Question

given the points A(-3,-5) and B (5,0), find the coordinates of the point P on a directed line segment AB that partitions AB in the ratio 2:3

Answer 1

\rule{31em}{0.25pt} " src="
`image`

`image`

Answer 2

`((1)/(5),-3)`.

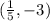Explanation:

We have been given the coordinates of points A(-3,-5) and B (5,0). We are asked to find the coordinates of the point P on a directed line segment AB that partitions AB in the ratio 2:3.

We will use section formula to solve our given problem. When a point P divides a line segment internally in ratio m:n, then coordinates of point P are:

`[x=(m\cdot x_2+n\cdot x_1)/(m+n);y=(m\cdot y_2+n\cdot y_1)/(m+n)]`

Upon substituting coordinates of our given points in section formula we will get,

`[x=(2\cdot 5+3\cdot -3)/(2+3);y=(2\cdot 0+3\cdot -5)/(2+3)]`

`[x=(10-9)/(5);y=(0-15)/(5)]`

`[x=(1)/(5);y=(-15)/(5)]`

`[x=(1)/(5);y=-3]`

Therefore, the coordinates of point P are
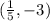`((1)/(5),-3)`.