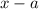 is a polynomial of degree 1, and as such it cannot be factorized.
is a polynomial of degree 1, and as such it cannot be factorized.
In fact, when you factor a polynomial
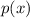 of degree
of degree
 , you write it as
, you write it as

So, if a polynomial is already of degree one, you should write it as a product of two polynomials, whose degrees sum to 1.
So, the only option would be
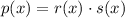
with
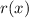 of degree 1 and
of degree 1 and
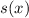 of degree 0, i.e. a constant polynomial, i.e. a simple number.
of degree 0, i.e. a constant polynomial, i.e. a simple number.
But this factorization is trivial, because it only allows you to write expressions like
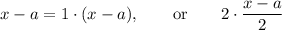
which are not actual polynomial factorizations.