Question

If the area of equilateral triangle abc is 4 times that of equilateral triangle pqr, then each side of abc is how many times the corresponding side of pqr?

Answer 1

For similar triangles

The ratio of the areas of the triangle is equal to the square of the ratio of the corresponding sides.

We know two equilateral are always similar.

Now it is given that area of ΔABC = 4 × ΔPQR

So
`(ABC)/(PQR)=(4)/(1)`

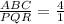
But according to the rule of similarity

`(ABC)/(PQR)= ((AB)/(PQ))^2`

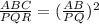
So we have

`((AB)/(PQ))^2=(4)/(1)`

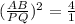
Taking square root on both sides

`(AB)/(PQ)=(2)/(1)`

`AB = 2PQ`

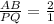
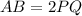
So each side of ΔABC is two times the side of ΔPQR.