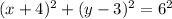Question

1. The beginning steps for determining the center and radius of a circle using the completing the square method are shown below:

Step 1
[original equation]: x2 − 6x + y2 − 4y = 3
Step 2
[group like terms]: (x2 − 6x) + (y2 − 4y) = 3
Step 3
[complete the quadratics]:


Which of the following is the correct equation for Step 3?
(x2 − 6x + 6) + (y2 − 4y + 4) = 4 + (6 + 4)
(x2 − 6x − 3) + (y2 − 4y − 2) = 4 + (−3 − 2)
(x2 − 6x + 3) + (y2 − 4y + 2) = 4 + (3 + 2)
(x2 − 6x + 9) + (y2 − 4y + 4) = 3 + (9 + 4)


2. Using the following equation, find the center and radius of the circle by completing the square.

x2 + y2 + 6x − 6y + 2 = 0

center: (−3, 3), r = 4
center: (3, −3) r = 4
center: (3, −3), r = 16
center: (−3, 3), r = 16



3. The beginning steps for determining the center and radius of a circle using the completing the square method are shown below:


Step 1
[original equation]: x2 + 8x + y2 − 6y = 11
Step 2
[group like terms]: (x2 + 8x) + (y2 − 6y) = 11
Step 3
[complete the quadratics]: (x2 + 8x + 16) + (y2 − 6y + 9) = 11 + (16 + 9)
Step 4
[simplify the equation]: (x2 + 8x + 16) + (y2 − 6y + 9) = 36
Step 5
[factor each quadratic]:


Which of the following is the correct equation for Step 5?
(x + 4)2 + (y − 3)2 = 62
(x + 8)2 + (y − 6)2 = 62
(x − 4)2 + (y + 3)2 = 62
(x + 16)2 + (y + 9)2 = 62

Answer 1

Answer :
`(x^2 - 6x + 9) + (y^2- 4y + 4) = 3 + (9 + 4)`

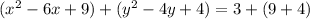
Center is (-3,3) and radius = 4

`(x + 4)^2 + (y - 3)^2 = 6^2`

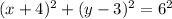
(1) Step 1:
`x^2 - 6x + y^2 - 4y = 3`

Step 2:
`(x^2- 6x) + (y^2 - 4y) = 3`

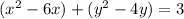
In completing the square method we take coefficient of x and divide by 2 and the square it . Then add it on both sides

The coefficient of x is -6.
`(-6)/(2)` = (-3)^2 = 9

The coefficient of y is -4.
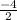`(-4)/(2)` = (-2)^2 = 4

Step :
`(x^2- 6x + 9) + (y^2 - 4y + 4) = 3 +9 + 4`

(2)
`x^2 + y^2 + 6x - 6y + 2 = 0`

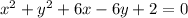
To find center and radius we write the equation in the form of

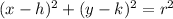`(x-h)^2 + (y-k)^2 = r^2` using completing the square form

Where (h,k) is the center and 'r' is the radius

`x^2 + y^2 + 6x - 6y + 2 = 0`

`(x^2 + 6x) + (y^2 - 6y) + 2 = 0`

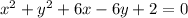
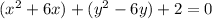
In completing the square method we take coefficient of x and divide by 2 and the square it . Then add it on both sides

`(x^2 + 6x + 9) + (y^2 - 6y + 9) = -2 + 9 + 9`

`(x + 3)^2 + (x - 3)^2 = 16`

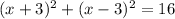
Here h= -3 and k=3 and
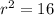`r^2 = 16` so r= 4

Center is (-3,3) and radius = 4

(c) Step 1:
`x^2 + 8x + y^2 - 6y = 11`

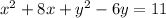
Step 2:
`(x^2 + 8x) + (y^2 - 6y) = 11`

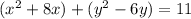
Step 3:
`(x^2 + 8x + 16) + (y^2 - 6y + 9) = 11 + (16 + 9)`

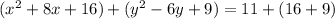
Step 4:
`(x^2 + 8x + 16) + (y^2 - 6y + 9) = 36`

We factor out each quadratic

(x^2 + 8x + 16) = (x+4)(x+4) =
`(x+4)^2`

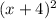
((y^2 - 6y + 9)) = (x-3)(x-3) =
`(x-3)^2`

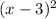
Step 5 :
`(x + 4)^2 + (y - 3)^2 = 6^2`