Question

Line segment SU is a diameter of circle V.

What is the measure of arc S T?

56°
68°
112°
163° (it is 56!)

Answer 1

A. 56 degrees

Explanation:

Just took the Unit Test on Edg (2021)!!

Answer 2

Answer: 112°

Explanation:

Angles in a Circle

An inscribed angle is formed between two chords whose vertices lie on the circumference of a circle. The figure shows three chords: TU, SU, and ST. SU happens to also be a diameter because it goes through the center of the circle V.

ST and SU form an inscribed angle of 34°. The corresponding central angle is TVU and its measure is

`m\angle TVU=2*34^\circ=68^\circ`

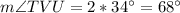
The required measure of the arc ST is the measure of the angle SVT. Note that SVT and TVU are complementary, thus:

`m\angle TVU+m\angle SVT=180^\circ`

Solving for the measure of SVT:

`m\angle SVT=180^\circ-m\angle TVU`

`m\angle SVT=180^\circ-68^\circ=112^\circ`

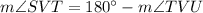
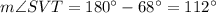
Answer: 112°