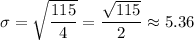Question

PLEASE HELP MEEEEEE!!

The data below show the number of hours Mrs. Diaz volunteered at the library each month for eight months. The mean of the data set is 22 hours. What is the mean
absolute deviation of the data?
The hours: 20, 12, 27, 23, 18, 20, 30, 26

Answer 1

4.5

i did it

Explanation:

Answer 2

To compute the standard deviation, we first need the array of distances from the mean. So, we consider the difference between each element of the dataset and the mean:

`20-22, 12-22, 27-22, 23-22, 18-22, 20-22, 30-22, 26-22`

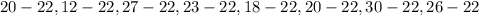
which is

`-2, 10, 5, 1, -4, -2, 8, 4`

Then, we need to square this array:

`4, 100, 25, 1, 16, 4, 64, 16`

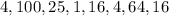
Then, we consider the mean of this new array, so we sum its components and divide by the number of elements:

`(4+ 100+ 25+ 1+ 16+4+ 64+ 16)/(8) = (230)/(8) = (115)/(4)`

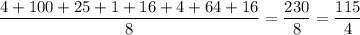
This is the variance, i.e. the standard deviation squared. So, we only need to take the square root of the variance to get the standard deviation:

`\sigma = \sqrt{(115)/(4)} = (√(115))/(2) \approx 5.36`