Question

A rectangular field has dimensions of (2x-3) yards and (x+4) yards. the area of the field is 285 square yards. what are the length and width of the field?

Answer 1

The area of a rectangle is given by the multiplication of its dimensions:

`\text{Area} = \text{width} * \text{length}`

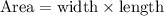
In this case, we have an exact value for the area, and two variable expressions for width and length. Let's replace the formula above with what we're given:

`285 = (2x-3)(x+4)`

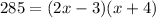
If you expand the right hand side, you have

`285 = 2 x^2+ 5 x-12`

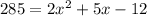
And if you move all terms to the right hand side, this becomes

`0 = 2 x^2+ 5 x-297`

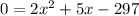
This is a quadratic equation, since it is in the form
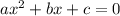`ax^2+bx+c=0`, where
`a = 2,\ b=5 \text{ and } c = -297`

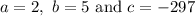
If you plug these values in the generic formula

`x_(1,2) = (-b\pm√(b^2-4ac))/(2a)`

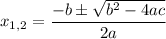
you get

`x = (-27)/(2) \text{ or } x = 11`

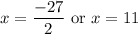
Let's see which dimensions they yield:

`x = (-27)/(2) \implies 2x-3 = -30,\quad x+4 = (-19)/(2)`

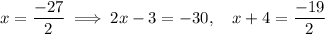
But the dimensions of a rectangle can't be negative, so we can't accept this answer.

The other solution yields

`x = 11 \implies 2x-3 = 19,\quad x+4 = 15`

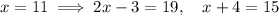
So these are the dimensions of the rectangle