You can find the equation of a line if you know the slope of the line and one point on the line using the point-slope form of the equation of a line.
First, let's find a point on the line. We will find the x-intercept. At the x-intercept, y = 0, so let y = 0 and solve for x.
g(x) = x^3 - 1
x^3 - 1 = 0
x^3 = 1
x = 1
The value of x at the x-intercept is 1, so the x-intercept is point (1, 0). We have the point we need.
Now we need the slope. The slope of this function at any point x is given by 3x^2. Let's find the slope at the x-intercept. At the x-intercept, x = 1, so the slope is
m = 3x^2 = 3(1)^2 = 3
We know the tangent line at the x-intercept has slope 3 and passes through the point (1, 0). Now we use the point-slope form of the equation of a line to find the equation of the tangent.
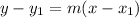
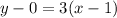
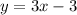
Answer: y = 3x - 3