Question

Suppose the coordinate of a is 0, ar = 5, and at =7. What are the possible coordinates of the midpoint of rt ?

Answer 1

Here 'a' corresponds to 0.

Now there are two possibilities for 'r' & 't'

Case 1.

They are on the same side to the right of 'a'

In that case 'r' corresponds to 5 & 't' corresponds to 7.

The midpoint of 'r' and 't' shall be
`(5+7)/(2) =6`

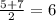
Case 2.

Both are on the left of 'a'.

In that case 'r' corresponds to -5 & 't' corresponds to -7

The midpoint shall be
`(-7-5)/(2) =-6`

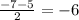
Case 3.

'r' in on the right of 'a' and 't' is on the left of 'a'

So 'r' corresponds to 5 and 't' corresponds to -7

The midpoint shall be
`(-7+5)/(2)=-1`

Case 4.

'r' is on the left of 'a' & 't' is on the right of 'a'.

'r' corresponds to -5 & 't' corresponds to 7

The midpoint shall be
`(-5+7)/(2)=1`

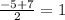
The possible coordinates of the midpoints of rt are 6, -6, 1, -1.