First step is to simplify the inside of the radical. There are x's on both top and bottom of the fraction. So we subtract their exponents. x³ - x¹ = x². Because the x³ was in the denominator and it was bigger, the x² goes on the bottom.
Your new equation is:
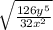
Now, I'd suggest factoring each term to correspond with the square root.
126y⁵ = 9 · 14 · y² · y² · y
32x² = 4 · 4 · 2 · x²
9, y², and y² can be square rooted in the numerator. 4, 4, and x² in the denominator. So we pull out their square roots and place them outside of the radical. The rest stays in the radical:
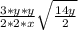
Simplify to get your final answer:
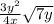
It's easier to explain on paper and in person than over computer text, sadly. Hopefully you can follow along with this.