If p and q are both true, then which of the following statements has the same truth-value as ~p → q? A) ~p ∧ ~q B) ~p ∨ ~q C) p ∧ ~q D) ~q → p

Question

asked Nov 20, 2019 38.8k views

1 Answer

Genericrich · Answer 1 · 2019-11-25T17:21:28+0000

If p and q are both true, then

$\\eg p \implies q$

is an implication of the form

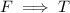
$F \implies T$

which is true, because every implication starting with false is true, i.e.

$F \implies T = T,\quad F \implies F = T$

So, we're looking for an expression evaluating to true. Let's see what we have:

A) is an AND proposition. Logical AND is true only if both parts are true. So, you have

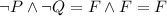
$\\eg P \land \\eg Q = F \land F = F$

So it's not the right option.

B) is an OR proposition. Logical OR is true whenever one of the two parts is true. So, you have

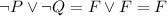
$\\eg P \lor\\eg Q = F \lor F = F$

So it's not the right option.

C) is again an AND proposition. You have

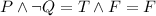
$P \land \\eg Q = T \land F = F$

So this is not the right option.

D) Finally, the last one is again an implication, and again it starts with false:

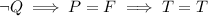
$\\eg Q \implies P = F \implies T = T$

So this is true, and thus is the correct option.