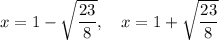Answer:
The zeroes of the given polynomial f(x) are
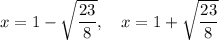
Explanation:
Given : Quadratic function
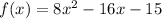
To find : What are the zeros of the quadratic function?
Solution :
Using quadratic formula of the general equation
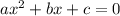 to get the roots is
to get the roots is
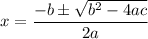
Comparing the given quadratic equation,
a = 8, b = -16 and c = - 15.
Substitute the value in the formula,

Therefore, The zeroes of the given polynomial f(x) are