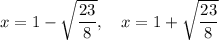Question

What are the zeros of the quadratic function f(x) = 8x2 – 16x – 15?

x = –1 – and x = –1 +
x = –1 – and x = –1 +
x = 1 – and x = 1 +
x = 1 – and x = 1 +

Answer 1

8x^2 - 16x - 15 = 0

x = [ -(-16) +/- sqrt((-16)^2 - 4*8*-15) / ] 2*8

= 2.696, -0.696

Answer 2

The zeroes of the given polynomial f(x) are

`x=1-\sqrt{(23)/(8)},~~~x=1+\sqrt{(23)/(8)}`

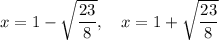
Explanation:

Given : Quadratic function
`f(x)=8x^2-16x-15`

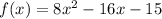
To find : What are the zeros of the quadratic function?

Solution :

Using quadratic formula of the general equation
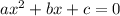`ax^2+bx+c=0` to get the roots is
`x=(-b\pm√(b^2-4ac))/(2a)`

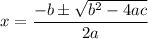
Comparing the given quadratic equation,

a = 8, b = -16 and c = - 15.

Substitute the value in the formula,

`x=(-b\pm√(b^2-4ac))/(2a)\\\\\\\Rightarrow x=(-(-16)\pm√((-16)^2-4* 8* (-15)))/(2* 8)\\\\\\\Rightarrow x=(16\pm√(256+480))/(16)\\\\\\\Rightarrow x=(16\pm√(786))/(16)\\\\\\\Rightarrow x=(16\pm4√(46))/(16)\\\\\\\Rightarrow x=(4\pm√(46))/(4)\\\\\\\Rightarrow x=1\pm\sqrt{(46)/(16)}\\\\\\\Rightarrow x=1\pm\sqrt{(23)/(8)}\\\\\\\Rightarrow x=1-\sqrt{(23)/(8)},~~~x=1+\sqrt{(23)/(8)}.`

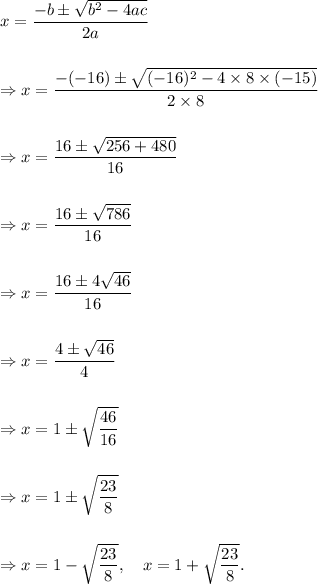
Therefore, The zeroes of the given polynomial f(x) are

`x=1-\sqrt{(23)/(8)},~~~x=1+\sqrt{(23)/(8)}`