The locus of all points k units away from (3, -1, -2) is the sphere
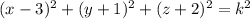
The locus of all points 2k units away from (-2, 3, 4) is the sphere
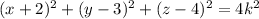
So, all points in the intersection of these two spheres are k units away from (3, -1, -2) and 2k units away from (-2, 3, 4), and thus they are twice as far from (-2, 3, 4) as from (3, -1, -2), as required.
If we divide the second equation by 4, we have
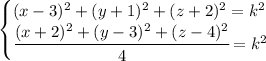
Since both left sides equal
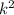 , they must be equal to each other:
, they must be equal to each other:
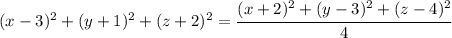
This equation describes the locus you're looking for.