Question

1) their slopes are equal but y-intercepts are not equal

2) their slopes are not equal but y-intercepts are equal
3) both slopes and y-intercepts are equal
4) neither slopes nor y-intercepts are equal

Answer 1

Function A describes f(x) = 5x + 2. ('2 more than' means 'add 2', and '5 times x' means '5x'.)

To find function B, calculate the slope using two of the given points in the table.

`(y - y)/(x - x) =(2-5)/(-1-0)=(-3)/(-1)=3`

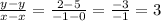
This creates a partial equation: y = 3x + b. To find b (or the y-intercept), input one coordinate pair from the chart.

`y=3x+b`

`2=3(-1)+b`

`2=-3+b`

`5 = b`

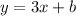
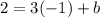
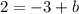
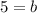
This creates the equation of function B: y = 3x + 5.

Now, you can compare the slopes and y-intercepts of function A and function B.

Function A: f(x) = 5x + 2

Function B: f(x) = 3x + 5

These functions do not share a slope nor a y-intercept.

Answer 2

neither slopes not y-intercept are equal