Question

Amazing Gadget Corporation has determined a quadratic relationship between its selling price for its newest tablet and the company's daily profit. Which of the following would be a reasonable estimate of the rate of change for the interval 200 ≤ x ≤ 300?

A. 2
B.-2
C.1/3
D.-1/3

Answer 1

Answer: A) 2

Explanation:

Apez

Answer 2

Consider the Quadratic relationship, between its selling price for its newest tablet and the company's daily profit is given by,

f(x)= a x² + b x + c

Differentiating once

f'(x)= 2 a x + b

As, we have to find rate of change for the interval 200 ≤ x ≤ 300.

So, f(200)= 2 a ×200 + b= 400 a + b

f(300)= 2 a × 300 + b= 600 a + b

Rate of change for the interval 200 ≤ x ≤ 300

`=(f(b)-f(a))/(b-a)\\\\= (600 a + b-400 a -b)/(300-200)\\\\ =(200a)/(100)\\\\=2 a`

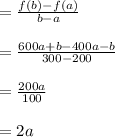
As considering , if the company is going through Profit, when the selling of the tablet is in the interval (200 ≤ x ≤ 300),

So, Reasonable estimate of the rate of change for the interval 200 ≤ x ≤ 300 considering if the company is making profit=2 →→Option (A)