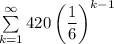
The infinite geometric series is converges if |r| < 1.
We have r=1/6 < 1, therefore our infinite geometric series is converges.
The sum S of an infinite geometric series with |r| < 1 is given by the formula :

We have:
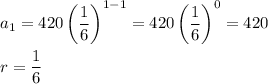
substitute:
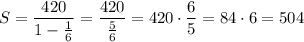
Answer: d. Converges, 504.