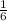Question

CONDITIONAL PROBABILITY URGENT?

Answer 1

WE need to find the probability (
`(Junior)/(Boy)`

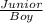
We know
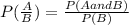
`P((A)/(B))= (P(A and B))/(P(B))`

P(
`(Junior)/(Boy)`)=
`(P(Junior and Boy))/((Boy))`

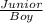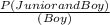
First we find P(Boy)

From the table we can see that we have 12 boys out of (12+18=30) students

So P(Boy) =
`(12)/(30)`

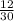
Now we find the intersection of Junior and Boy

WE look at the Junior row and boys column that is 2

{P(Junior ∩ Boy) =
`(2)/(30)`

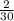
P(
`(Junior)/(Boy)`)=
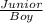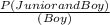
`(P(Junior and Boy))/((Boy))`

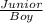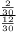
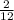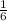
P(
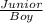`(Junior)/(Boy)`)=
`((2)/(30))/((12)/(30))`

=
`(2)/(12)` =
`(1)/(6)`

P(
`(Junior)/(Boy)`) =
`(1)/(6)`