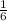WE need to find the probability (
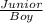
We know
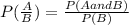
P(
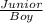 )=
)=
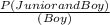
First we find P(Boy)
From the table we can see that we have 12 boys out of (12+18=30) students
So P(Boy) =
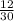
Now we find the intersection of Junior and Boy
WE look at the Junior row and boys column that is 2
{P(Junior ∩ Boy) =
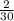
P(
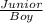 )=
)=
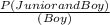
P(
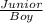 )=
)=
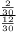
=
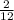 =
=
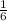
P(
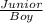 ) =
) =