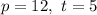Question

My friend and I both have the same math homework one day. I work at a rate of $p$ problems per hour and it takes me $t$ hours to finish my homework. My friend works at a rate of $2p-4$ problems per hour and it only takes him $t-2$ hours to finish his homework. Given that $p$ and $t$ are positive whole numbers and I do more than $10$ problems per hour, how many problems did I do?

Answer 1

why are you booing him? he's right

12 * 5 = 60

ok?

60

smh

Answer 2

If you do
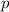`p` problems per hour, after
`t` hours you do
`pt` problems.

Similarly, your friend does
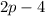`2p-4` problems per hour, so after
`t-2` he has completed
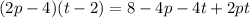`(2p-4)(t-2) = 8 - 4p - 4t + 2pt` problems.

Since you have the same number of problems, we deduce

`pt = 8 - 4p - 4t + 2pt`

which we can rewrite as

`8 - 4p - 4t + pt = 0`

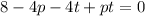
If we solve this equation for one of the two variables, for example t, we have

`t = \cfrac{4(p-2)}{p-4}`

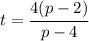
Since p and t are positive integers, p must be at least 4.

Finding integers solutions require a bit of trial and error, and you can figure out that the only positive and integer solution where p > 10 is

`p=12,\ t=5`