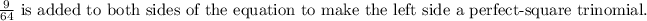Answer:
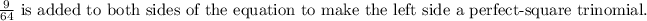
Explanation:
Given the equation
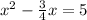
we have to find the value which must be added to both sides of the equation to make the left side a perfect-square trinomial.
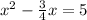
To form the perfect square we have to add the square of half the coefficient of x,
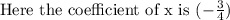
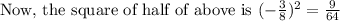
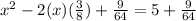
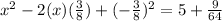
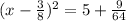
which makes LHS a perfect square trinomial.