Answer: The correct option is tan(F).
Step-by-step explanation:
In the given figure the triangle is a right angle triangle because
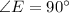 .
.
It is also given that
 and
and
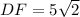 .
.
Since it is an isosceles right angle triangle, therefore the value of perpendicular and base is same for both angles D and F, which is 5.
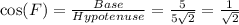
The value of cos(F) is
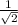 .
.
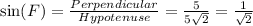
The value of sin(F) is
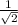 .
.
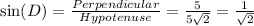
The value of sin(D) is
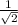 .
.
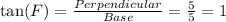
The value of tan(F) is 1. Which is not equal to
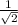 .
.
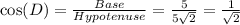
The value of cos(D) is
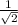 .
.
Therefore, the value of tan(F) is not equal to the value of cos(F), so the correct option is third.