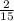Question

an urn contains balls numbered 1 to 15 a ball is chosen returned to the urn and the second ball is chosen what is the probability that the first and the second of all will be a six

Answer 1

1/30 chance I think. 1/15 and 1/15

Answer 2

`(2)/(15)`

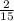
Explanation:

An urn contains balls numbered from 1 to 15

Total number of outcomes= 15

Let E1 be event of getting a ball numbered 6

Favorable case to E1= 1

Probability=
`(favourable case)/(total number of outcomes)`

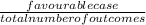
P(E1)=
`(1)/(15)`

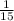
A ball is chosen and returned to urn

Again, total number of outcomes=15

Let E2 be event of getting a ball numbered 6

Favorable case to E2= 1

P(E2)=
`(1)/(15)`

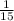
The Probability that the first and second ball is 6=P(E1)+P(E2)

=
`(1)/(15)`+
`(1)/(15)`

=
`(2)/(15)`

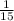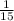
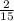
Hence, the correct answer is
`(2)/(15)`