Let's start from the parent function
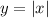 and see which transformation we have applied. The parent function's graph is open upards, and its vertes lies at
and see which transformation we have applied. The parent function's graph is open upards, and its vertes lies at
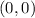
The first transformation is
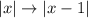 . This is a tranformation of the form
. This is a tranformation of the form
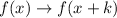 . This kind of transformation shift the graph horizontally, k units to the left if k is positive, k units to the right if k is negative. In this case
. This kind of transformation shift the graph horizontally, k units to the left if k is positive, k units to the right if k is negative. In this case
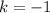 , so the function is shifted one unit to the right. The new vertex lies at
, so the function is shifted one unit to the right. The new vertex lies at
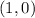
The second transformation is
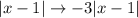 . This is a tranformation of the form
. This is a tranformation of the form
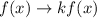 . This kind of transformation stretch the graph vertically, compressing it if k is between 0 and 1, expanding it if k is greater than 1. Moreover, if k is negative, the function is reflected along the x axis. In this case
. This kind of transformation stretch the graph vertically, compressing it if k is between 0 and 1, expanding it if k is greater than 1. Moreover, if k is negative, the function is reflected along the x axis. In this case
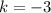 , so the function is reflected and stretched. This means that now the graph opens downwards, the vertex still lies at
, so the function is reflected and stretched. This means that now the graph opens downwards, the vertex still lies at
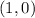 .
.
Finally, we have
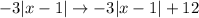 . This is a tranformation of the form
. This is a tranformation of the form
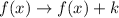 . This kind of transformation translates the graph vertically, k units up if k is positive, k units down if k is negative. In this case,
. This kind of transformation translates the graph vertically, k units up if k is positive, k units down if k is negative. In this case,
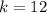 , so the graph is shifted 12 units up. The graph still opens downwards, while the new vertex lies at
, so the graph is shifted 12 units up. The graph still opens downwards, while the new vertex lies at
