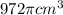Given, the surface area of a sphere is =
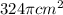
The formula to find the surface area of a sphere =

Where, r is the radius of the sphere.
As the surface area of the sphere given, we can equate it with the formula.
So we can write the equation as,
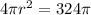
To find r, first we have to move 4 to the right side by dividing it to both sides. We will get,
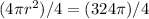
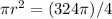

Now to find r, we have to move
 to the right side, by dividing it to both sides. We will get,
to the right side, by dividing it to both sides. We will get,
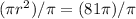
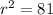
Now to find r, we will take square root to both sides.
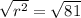
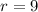
So we have got the radius of the sphere = 9cm.
Now the formula to find the volume of the sphere =
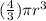
Now plugging in the value of r we will get,
Volume =
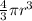
=
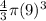
=

=
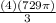
=
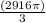
=
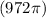
So the required volume of the sphere =