Question

Find x∈R:

|x-1|+|x-4|=3
An explanation would be helpful, as I don't know how to solve it.
Thank you!

Answer 1

Whenever you find an equation involving absolute values, you have to think that you're actually multiple different equations. The absolute values work as a switch, "activating" one of the various form of the equation.

In fact, the absolute value always returns the positive version of the quantity it holds, as in

`|x| = \begin{cases} x &\text{if } x\geq 0\\ -x &\text{if } x < 0 \end{cases}`

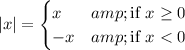
In your case, this means that

`|x-1| = \begin{cases} x-1 &\text{if } x-1\geq 0 \iff x\geq 1\\ -x+1 &\text{if } x < 1 \end{cases}`

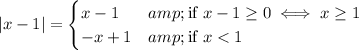
and

`|x-4| = \begin{cases} x-4 &\text{if } x-4 \geq 0 \iff x\geq 4\\ -x+4 &\text{if } x < 4 \end{cases}`

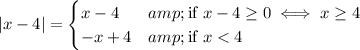
So, we can split the real numbers in three different zones: if
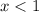`x < 1`, both expressions are negative, so you have
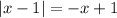`|x-1| = -x+1` and
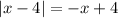`|x-4| = -x+4`. Otherwise, if
`1\leq x<4`,
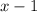`x-1` is positive, while
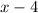`x-4` is still negative. This means that
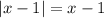`|x-1| = x-1` and
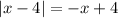`|x-4| = -x+4`. Finally, if
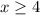`x\geq 4`, then both quantities are positive, and the absolute values won't change them:
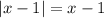`|x-1| = x-1` and
`|x-4| = x-4`.

As you may imagine, we have three different equations, depending on which part of the real number line we're considering:

First zone: x < 1

Given everything we've said about how to solve absolute values, in this area the equation becomes

`-x+1-x+4=3 \iff -2x+5=3 \iff -2x = -2 \iff x = 1`

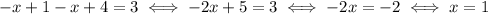
But we are assuming that
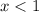`x < 1`, so we can't accept this solution.

Second zone:
`1 \leq x < 4`

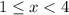
In this area the equation becomes

`x-1-x+4=3 \iff 3 = 3`

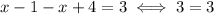
Which is always true. All numbers in
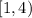`[1,4)` are a solution of this equation.

Third zone:
`x \geq 4`

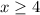
In this area the equation becomes

`x-1+x-4=3 \iff 2x - 5 = 3 \iff 2x = 8 \iff x = 4`

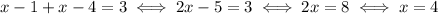
So, 4 is also a solution. The complete set of solutions is given by
`[1,4) \cup \{4\} = [1,4]`

So, all numbers between 1 and 4, 1 and 4 included, are solutions of this equation.