Whenever you find an equation involving absolute values, you have to think that you're actually multiple different equations. The absolute values work as a switch, "activating" one of the various form of the equation.
In fact, the absolute value always returns the positive version of the quantity it holds, as in
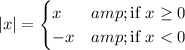
In your case, this means that
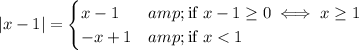
and
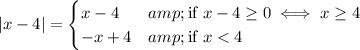
So, we can split the real numbers in three different zones: if
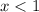 , both expressions are negative, so you have
, both expressions are negative, so you have
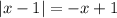 and
and
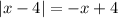 . Otherwise, if
. Otherwise, if
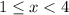 ,
,
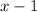 is positive, while
is positive, while
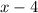 is still negative. This means that
is still negative. This means that
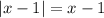 and
and
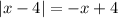 . Finally, if
. Finally, if
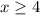 , then both quantities are positive, and the absolute values won't change them:
, then both quantities are positive, and the absolute values won't change them:
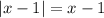 and
and
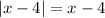 .
.
As you may imagine, we have three different equations, depending on which part of the real number line we're considering:
First zone: x < 1
Given everything we've said about how to solve absolute values, in this area the equation becomes
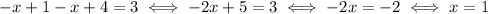
But we are assuming that
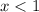 , so we can't accept this solution.
, so we can't accept this solution.
Second zone:
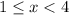
In this area the equation becomes
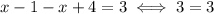
Which is always true. All numbers in
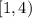 are a solution of this equation.
are a solution of this equation.
Third zone:
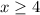
In this area the equation becomes
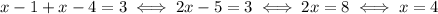
So, 4 is also a solution. The complete set of solutions is given by
![[1,4) \cup \{4\} = [1,4]](https://img.qammunity.org/2019/formulas/mathematics/high-school/8yk7r4nizlkgz66bn7baomuftdx3knapsm.png)
So, all numbers between 1 and 4, 1 and 4 included, are solutions of this equation.