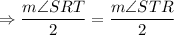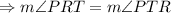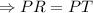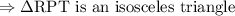Answer:
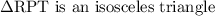
Explanation:
As in the triangle RST,
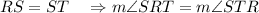
Because if in a triangle two angles equal one another, then the sides opposite the equal angles also equal one another.
Incenter is obtained by the Intersection of a triangle's three angle bisectors and it is equidistant from the three sides of the triangle.
So, RP and TP are the angle bisectors of ∠R and ∠T respectively.