Question

Andrea added 0.45 to 0.333 and made the conclusion that the sum of two rational numbers is rational. Is Andrea correct? Explain

Answer 1

She's correct, but not for the right reasons. The sum of any two rational numbers is rational, but simply giving one example of that being the case isn't enough. In fact, Andrea could have done billions of similar cases and always found that there was one case she hadn't tested. What we need here is a proof, and here it is.

Let's say we have two rational numbers
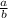`(a)/(b)` and
`(c)/(d)`, where a, b, c, and d are all integers. Adding the two numbers together, we find that their sum is

`(a)/(b)+(c)/(d)=(a)/(b)\big((d)/(d)\big)+(c)/(d)\big((b)/(b)\big)=(ad)/(bd)+(cb)/(bd)=(ad+cb)/(bd)`

Since the sum or product of any two integers is always another integer, we know that both ad + cb and bd are integers, and since the definition of a rational number is a ratio of two integers, we can say with 100% certainty that
`(ad+cb)/(bd)` is rational, which means that the sum of any two rational numbers is also rational.