Answer:
The common ratio for the geometric sequence is:
2
Explanation:
In general, the terms of geometric sequence is given as:
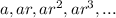
where a is the first term and r is the common ratio
Here, a=3
and fifth term of geometric sequence=48
i.e.
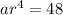
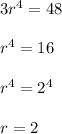
Hence, the common ratio for the geometric sequence is:
2