Question

A carpenter is assigned the job of expanding a rectangular deck where the width is one-fourth the length. the length of the deck is to be expanded by 10 feet, and the width by 6 feet. if the area of the new rectangular deck is 128 ft2 larger than the area of the original deck, find the dimensions of the original deck

Answer 1

Alright, lets get started.

Suppose the original deck size: width = x feet

the width is one-fourth the length given in question means length = 4 x feet

Means the originally area =
`x * 4 x = 4 x^(2)`

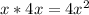
Now the dimensions are changed.

New dimensions, width = (x + 6)

new length = (4x+10)

So, new area will be =
`(x+6) * (4x+10) = 4x^(2) + 10 x + 24 x + 60 = 4x^(2) + 34 x + 60`

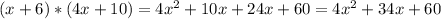
the area of the new rectangular deck is 128 ft2 larger than the area of the original deck, means

`4x^(2) + 128= 4x^(2) + 34 x + 60`

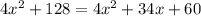
Subtracting
`4x^(2)` from both sides

`128 = 34 x + 60`

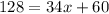
Subtracting 60 from both sides

`128 - 60 = 34 x + 60 - 60`

`68 = 34 x`

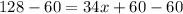
Dividing 34 in both sides

`(68)/(34) = (34 x )/(34)`

`x = 2`

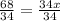
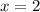
Means width = 2 feet

Length would be = 4 time width = 4 * 2 = 8 feet

Means dimension of original deck would be = 2 feet and 8 feet :Answer

Hope it will help :)