Answer:
The third graph represents the function
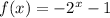
Explanation:
We have the function,
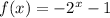 .
.
As we know, 'The y-intercept of a function is the point where the graph of the function crosses y-axis'.
i.e. At x=0, we get the y-intercept is
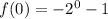 i.e.
i.e.
 i.e. f(0) = -2.
i.e. f(0) = -2.
So, the y-intercept of the function is at (0,-2).
Since, out of the four graphs given, we see that, the third graph crosses y-axis at (0,-2).
Moreover, as
 , then
, then
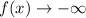 and
and
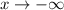 , then
, then
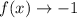
Hence, the third graph represents the function
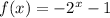 .
.