Question

Write and then solve for the differential equation for the statement: "The rate of change of y with respect to x is inversely proportional to y2."

Is this correct?
y'=1/y2
y2dy=dx
y3/3+C=x

Answer 1

Given that the rate of change of y with respect to x is inversely proportional to y². Its equation can be written as :-

`(dy)/(dx) = (k)/(y^(2))`

where 'k' is the proportionality constant, it can take any real value.

We can solve it by integrating the above equation with respect to x.

Rewriting and rearranging the terms of above equation :-

`(dy)/(dx) = (k)/(y^(2))`

y²·dy = k·dx

Integrating both sides :-

∫ y²·dy = ∫ k·dx

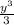`(y^(3))/(3)` = k·x

y³ = 3·k·x + C

where C is the constant of integration.

So, y³ = 3·k·x + C is the final answer.