This question presents an interesting pattern.
The rule/pattern to be followed here is:
Left side of the number looking at the previous one: (First digit x Third digit + 1)
Right side: (Second digit x Fourth digit -1)
For example, let us take 6447. Let us look at it's previous number, 9876.
Now,
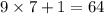 and
and
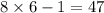
that is how we got 6447
Again, for the third number, 2527, let us look at it's previous number, 6447
Now,
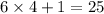
and
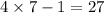
that is how we got 2527
Going by the same logic, the missing number should be 534.
This we got by applying the rule of the pattern as:
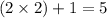
and

Thus, we got 534.