Question

True or false. Tan^2 x = 1 - cos2x/ 1 + cos 2x

Answer 1

True

Step-by-step explanation

The given trigonometric equation is

`\tan^(2) (x) = (1 - \cos(2x) )/(1 + \cos(2x) )`

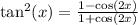
Recall the double angle identity:

`\cos(2x) = \cos^(2) x - \sin^(2)x`

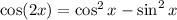
We apply this identity to obtain:

`\tan^(2) (x) = (1 - (\cos^(2) x - \sin^(2)x) )/(1 + (\cos^(2) x - \sin^(2)x) )`

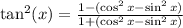
We maintain the LHS and simplify the RHS to see whether they are equal.

Expand the parenthesis

`\tan^(2) (x) = (1 - \cos^(2) x + \sin^(2)x )/(1 + \cos^(2) x - \sin^(2)x)`

`\implies\tan^(2) (x) = (1 - \cos^(2) x + \sin^(2)x )/(1 - \sin^(2)x + \cos^(2) x )`

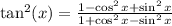
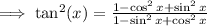
Recall that:

`1 - \sin^(2)x = \cos^(2)x`

`1 - \cos^(2)x = \sin^(2)x`

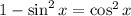
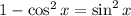
We apply these identities to get:

`\implies\tan^(2) (x) = (\sin^(2)x + \sin^(2)x )/(\cos^(2) x + \cos^(2) x )`

`\implies\tan^(2) (x) = (2\sin^(2)x )/( 2\cos^(2) x )`

`\implies\tan^(2) (x) = (\sin^(2)x )/( \cos^(2) x )`

`\implies \tan^(2) (x) =( (\sin x )/( \cos x ))^(2)`

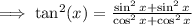
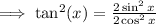
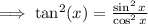
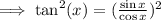
Also

`(\sin x )/( \cos x ) = \tan(x)`

`\implies \tan^(2) (x) =( \tan x )^(2)`

`\implies \tan^(2) (x) =\tan^(2) (x)`

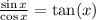
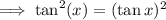
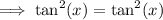
Therefore the correct answer is True