Answer:
Remaining volume of carved is 542.06 (approx 542) cm³
Explanation:
A sphere with a radius of 4.8 cm is carved out of a right cone with base of 8 cm and a height of 15 cm.
We need to find the remaining portion of the cone.
Remaining volume = Volume of cone - Volume of sphere
First we find volume of cone
Volume of cone
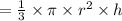
Volume of cone
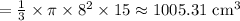
Now we find volume of sphere
Volume of sphere
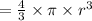
Volume of sphere
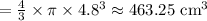
Remaining volume = 1005.31-463.25 = 542.06 cm³
Hence, Remaining volume of carved is 542.06 cm³