Question

Suppose that the height (in centimeters) of a candle is a linear function of the amount of time (in hours) it has been burning. After 9 hours of burning, a candle has a height of 24.5 centimeters. After 23 hours of burning, its height is 17.5 centimeters. What is the height of the candle after 21

hours?
___ centimeters

Answer 1

Suppose that the height (in centimeters) of a candle is a linear function of

the amount of time (in hours) it has been burning.

Let x be the amount of time in hours

Let y be the heoght of a candle in centimeters

The two points are then as (9,24.5) and (23,17.5).

`\mathrm{Find\:the\:line\:}\mathbf{y=mx+b}\mathrm{\:passing\:through\:}\left(9,\:24.5\right)\mathrm{,\:}\left(23,\:17.5\right)`

`\mathrm{Slope\:between\:two\:points}:\quad \mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

`\left(x_1,\:y_1\right)=\left(9,\:24.5\right),\:\left(x_2,\:y_2\right)=\left(23,\:17.5\right)`

`m=(17.5-24.5)/(23-9)`

`m=-0.5`

`\mathrm{Plug\:the\:slope\:}-0.5\mathrm{\:into\:}y=mx+b`

`y=\left(-0.5\right)x+b`

`\mathrm{Plug\:in\:}\left(9,\:24.5\right)\mathrm{:\:}\quad \:x=9,\:y=24.5`

`24.5=\left(-0.5\right)\cdot \:9+b`

`24.5=\left(-0.5\right)\cdot \:9+b`

`-4.5+b=24.5`

`b=29`

`\mathrm{Construct\:the\:line\:equation\:}\mathbf{y=mx+b}\mathrm{\:where\:}\mathbf{m}=-0.5\mathrm{\:and\:}\mathbf{b}=29`

`y=-0.5x+29`

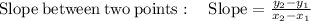
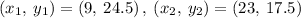
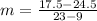
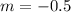
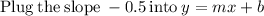
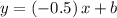
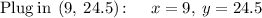
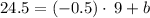
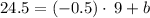
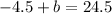
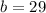
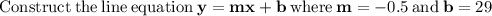
Now plug in x=21, we get

`y=-0.5*21+29=18.5`

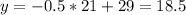
Thus the height of the candle after 21 hours is 18.5 centimeters.