Answer:

So we expect to win around 0.26 for each game that we play on this game.
Explanation:
For this case we can define a random variable who represent the amount of money win or loss X. X=1 if we got a head and X=-1 if we got a tail.
The expected value of a random variable X is the n-th moment about zero of a probability density function f(x) if X is continuous, or the weighted average for a discrete probability distribution, if X is discrete.
And from definition the expected value is defined with this formula:
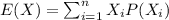
For this case we have the following probabilities:
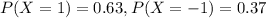
And then we can replace like this:

So we expect to win around 0.26 for each game that we play on this game.