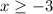Question

Find the domain of the following function:

\[ y=\sqrt{x} \]
\[y= \sqrt{x+3} \]

Answer 1

`y=√(x)`

As we know, the square root of negative numbers.

Hence, the x must be a positive value and greater than 0.

So, x:x∈[0,∞)

`y=√(x+3)`

`x+3\geq 0`

subtracting 3 from both sides

`x\geq -3`

x:x∈[-3,∞)

Answer 2

Firstly we have to determine the domain of the function
`y=√(x)`

The domain of the function is the set of values for which the function is real and defined.

In the function
`y=√(x)` we can clearly observe that for the negative values of x , the value of y will not be real.

So, the domain for this function is
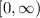`[0,\infty )` or
`x\geq 0`.

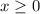The second function is
`y=√((x+3))`

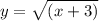
In this function we can clearly observe that for the values of x less than -3, the function is not real.

So, the domain for this function is
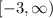`[-3,\infty )` or
`x\geq -3`